Arhitectură topologică

Topologia [gr. topos - loc, logos - studiu] este o ramură a matematicii care determină și studiază proprietățile fundamentale ale unor anumite tipuri de spații. Robert Bruner¹ susține că topologia este, de fapt, una dintre formele primare ale geometriei, care, deși reprezintă un domeniu distinct, este utilizată în aproape toate ramurile matematicii, sub o formă sau alta. Însușirile topologiei diferă de cele ale geometriei euclidiene. În timp ce geometria euclidiană se bazează pe cantități măsurabile precum distanțe, suprafețe, unghiuri, topologia lucrează cu structuri abstracte a căror caracteristică comună este continuitatea, una dintre proprietățile de bază ale spațiului. Când vorbim despre structuri abstracte, ne referim la acele tipuri de spații non-orientabile, ale căror proprietăți nu se modifică în cazul deformării și care folosesc invarianți precum conectivitatea și soliditatea.

Cea mai cunoscută structură topologică a fost descoperită în 1858 de către matematicianul german August Ferdinand Möbius. Este vorba despre banda lui Möbius, primul exemplu de suprafață non-orientabilă, ale cărei fețe sunt imposibil de deosebit. Dacă urmărim o traiectorie liniară pe axul central al acestei benzi, ajungem în punctul de unde am pornit, constatând faptul că banda reprezintă o unică suprafața continuă.

Dar cum se poate aplica topologia în practica arhitecturală? Datorită invarianților cu care lucrează, aplicarea topologiei în alte domenii, în afara matematicii sau informaticii, devine un procedeu abstract. Deoarece principalele caracteristici ale structurilor topologice sunt flexibilitatea și capacitatea de adaptare, matematicienii nu sunt convinși de aplicabilitatea topologiei în arhitectură. În cazul arhitecturii avem de a face cu materialitatea concretă, clădirile fiind caracterizate de rigiditate și stabilitate, proprietăți opuse topologiei. Însă arhitecții care adoptă abordarea topologică încearcă să găsească soluții pentru eliminarea rigidității obiectului construit, astfel încât, în funcție de anumiți factori, acesta să se poată adapta și să facă față unor situații diferite.

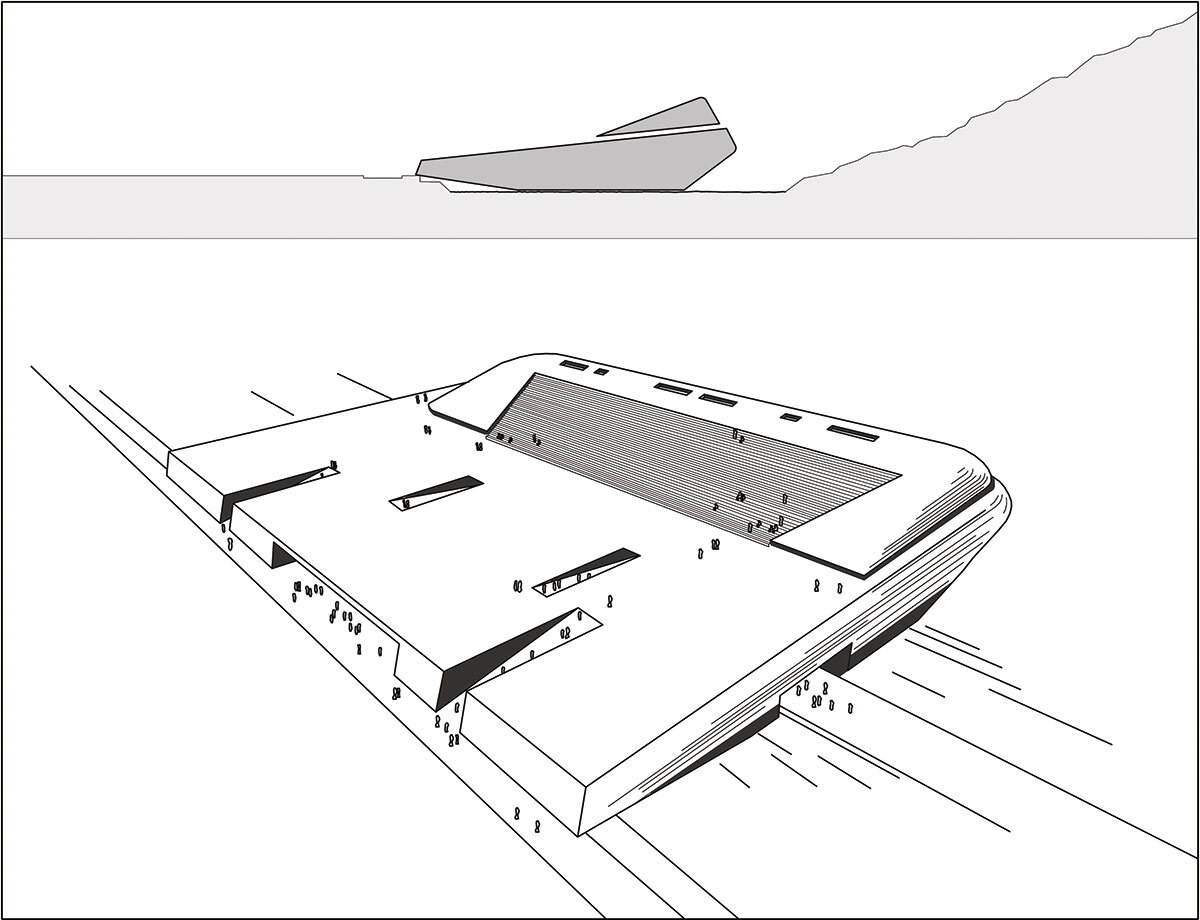
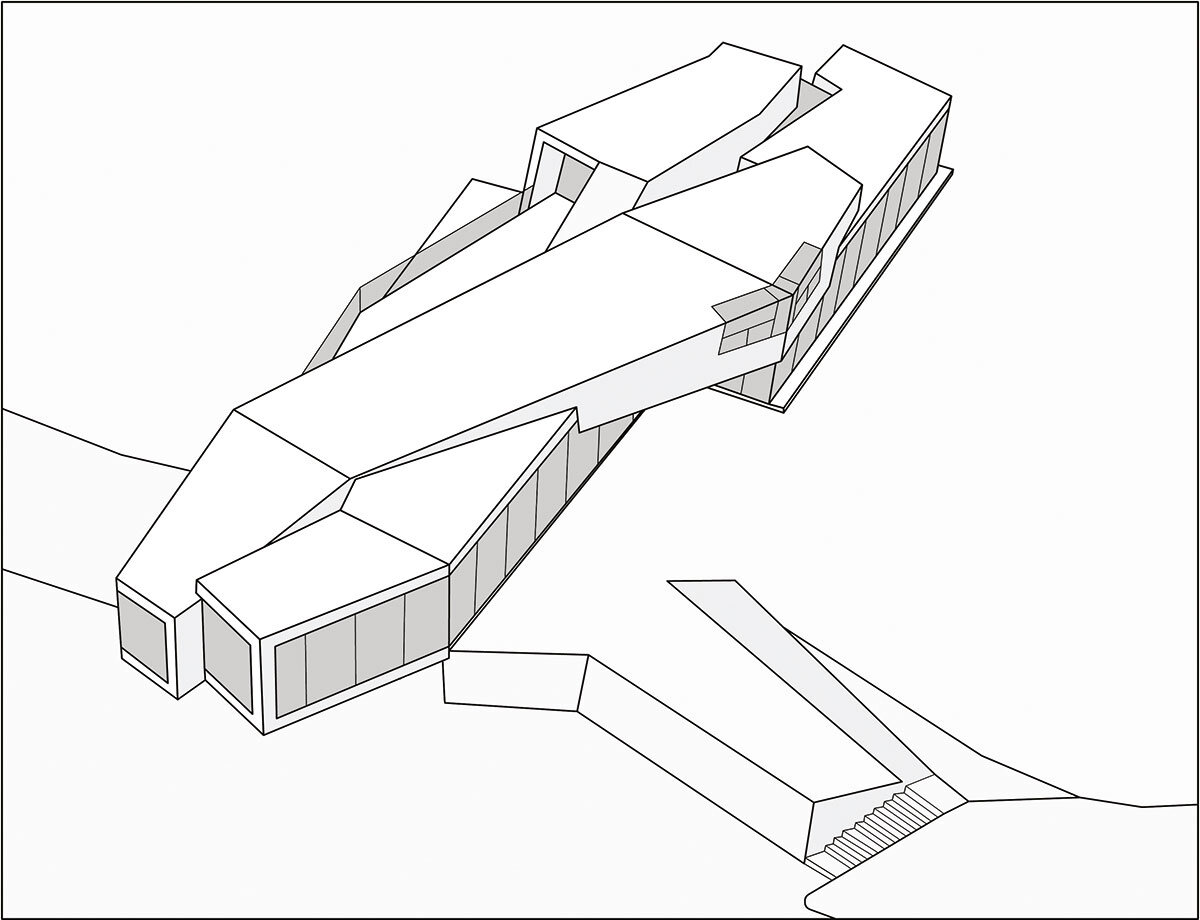
Introducerea noțiunii de topologie în arhitectură are loc la începutul anilor ‘60 odată cu formularea principiilor funcțiunii oblice de către Claude Parent și Paul Virilio², membri fondatori ai grupului Architecture Principe. Intenția celor doi a fost aceea de a depăși ortogonalitatea și de a se orienta spre o arhitectură bazată pe geometria non-euclidiană. Funcțiunea oblică a constituit o încercare de aplicare a topologiei în arhitectură, ce utiliza suprafețele oblice pentru a crea unitate și fluiditate între obiectul de arhitectură și context, facilitând o circulație locuibilă. Dincolo de aspectul estetic, funcțiunea oblică a condus către o destabilizare a obiectului modern, prin abstractizarea radicală, reprezentând o critică a verticalității și orizontalității adusă arhitecturii și urbanismului acelor timpuri. Una dintre primele propuneri ale lui Parent și Virilio, ce a urmărit această direcție, a fost Palatul de expoziții din Charleville³, din 1966, un program ce implica un amestec complex de activități culturale și comerciale. În cazul acestui proiect, autorii au căutat să promoveze alte tipuri de conexiuni, stabilind o nouă relație artificială cu relieful și cu spațiul înconjurător. Cei doi au încercat să definească un nou mod de parcurgere a spațiului, îndemnând către noi direcții și noi posibilități de folosire a suprafețelor.

Citiți textul integral în numărul 6 / 2014 al Revistei Arhitectura

NOTE:

1 Robert Bruner activează ca profesor de matematică în cadrul Universității de Stat Wayne.

2 Activitatea lui Parent (arhitect) și Virilio (teoretician) între 1963 și 1968 a reprezentat o provocare față de modernismul postbelic, atât ca limbaj formal, cât și ca discurs sociomoral. Ei au refuzat tot ceea ce era la modă și au cercetat prin intermediul proiectării, fiind într-o permanentă căutare a unor noi posibilități și tehnici de construcție.

3 Clădire de mari dimensiuni, concepută sub forma unei coji de beton și amplasată pe cursul râului Meuse; proiectul nu a fost realizat.